01
正确理解期权
期权并不像很多人所说的那样能够做到“期权在手,投资不愁。期权在手,天下我有”。很多由于对于对期权不理解或者不正当使用,导致了很大的风险,甚至导致公司倒闭的风险,因此正确地理解使用期权十分重要。
许多人初次接触期权,都会接触到“买方风险有限而收益无限,卖方收益有限而风险无限”的字眼。实际上,无论是风险还是盈利,无论是有限还是无限,都要分清理论和实际的区别。
首先,风险为盈亏与概率的乘积。卖方亏损理论上是无限的,但是如果概率很小,则风险就不大了;买方盈利是无限的,却没有实际胜算的把握,风险也不小,甚至可能亏损100%。而实际如何,就看投资者对行情的分析能力了。
其次,标的价格不可能跌至零,也不可能无限上涨,由此,“无限”的盈亏即使在实际上并不存在。但从资金管理的角度来讲,一旦价格发生较大的不利变化或者波动率大幅升高,对于卖方来说,此时的损失已相当于“无限”了。
因此,在进行期权投资之前,投资者一定要全面客观地认识期权交易的风险。
其实,期权就相当于保险,买期权所付的权利金相当于保险费,行情如果没有意外,你的最大损失是保险金;而发生意外的时候,就可以运用持有的期权而得到保护。卖期权就相当于卖保险,很多时候可以把卖期权得到的权利金收到兜儿里,如果行情出现大的以外,就要支付期权买方很大的费用。
02
期权该如何运用
虽然很多由于对于对期权不理解或者不正当使用,导致了很大的风险,但是期权在风险管理、风险度量等方面又有其独特的功能和作用。
从避险角度来讲,期权的策略主要包括套期保值和无风险套利。对于企业来讲还可以利用期权对经营管理人员进行激励,调动他们的的工作积极性。
1、套期保值
高杠杆带来的投机机会以及多合约之间的套利空间料将使得期权上市后备受关注,但作为衍生工具,期权在风险管理上也能发挥灵活的作用。譬如期权的套期保值,即配合期货或现货的头寸,用建立的期权部位的收益,弥补期货或现货可能出现的损失,以达到锁定价格变动风险的目的。
(1)期权买入套保策略
买期权为标的对冲,用较高的成本来为标的提供保护。
以股票为例,假设某投资者购买了5000股上汽集团的股票,在股价为20元的时候,投资者出于某种需求想在市场规避股价下跌的风险,若市场上有行权价为20元的期权合约,那么,可选择买入时间上相匹配的看跌期权,按照成交价格支付权利金,假设所买期权合约的权利金为0.5元。
那么投资者就通过看跌期权将股价下行的最大风险锁定,可以试想,若股价继续下跌至19元或者更低,在持有至到期后,投资者都有权利按照20元的价格将股票卖出。
所以,跌的越多,在期权上行权后的收益就越大,这部分的收益与持有正股的亏损可以相互抵消,从而达到规避风险的目的。另外,买入看跌期权的操作,还给予在股票价格上涨时仍能获利的空间,正股与看跌期权多头的组合收益类似于买入看涨期权。
之所以说买入期权是一种成本较高的对冲方式,因为投资者最初支付的权利金会影响最终的对冲效果,若持有至到期行权,期权买方将损失权利金,当然,实际操作中,投资者并非一定要将期权持有到期。
(2)期权卖出套保策略
卖出期权,用获得的权利金抵补正股的部分亏损。仍然沿用上面的例子,投资者除买入看跌期权为其持有的股票提供保护外,还可在市场上卖出看涨期权,不过,这样操作只能为股票提供部分保护。
假设所卖出的执行价格为20元的看涨期权成交价也为0.5元。在股票价格上涨时,正股获利,但看涨期权空头部位在达到损益平衡点(20.5)后开始出现亏损;正股下跌,出现亏损,看涨期权的最大收益为最开始收到的权利金。
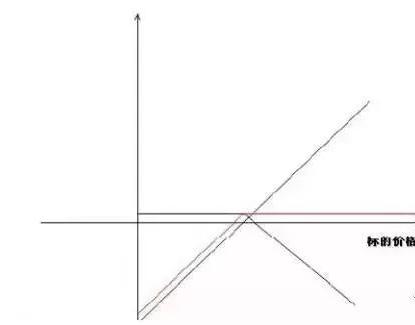
所以,很容易体会到,一旦价格出现大幅度的下跌,卖出看涨期权是无法达到较好的对冲效果。
通过买入看跌期权和卖出看涨期权为正股进行保值的操作对比,投资者可以感觉到二者的明显区别,总的来说是需要投资者在保值效果与成本之间权衡。
(3)双限策略套保
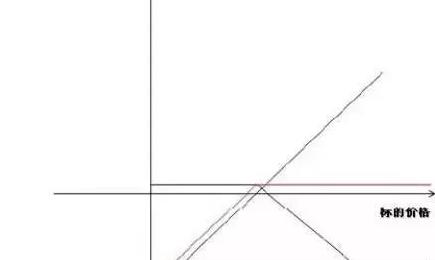
还有一种方式可以兼顾保值效果与成本,就是同时操作上面提到的两种头寸,即买入较低价位的看跌期权并卖出较高价位的看涨期权来为持有的股票保值。
买入看跌期权侧重于更全面的规避下行风险,卖出看涨期权则意在通过权利金收入减少保值成本。最终的损益图与牛市差价组合的结构类似,这种保值操作有时也叫双限交易策略。
因为投资者整体持仓的最大收益与最大风险均被控制在已知的范围内,与单纯的买入看跌期权套保相比,因为获得了成本上的优势,所以损失掉了大幅上涨的空间;而与单纯的卖出看涨期权保值相比,在提供下行保护上进行了优化,但成本也相对提高了。
应该说,三种方式并无绝对的利弊,具体如何选择应结合投资者的实际需求。
2、无风险套利
期权的无风险套利机会主要来源于期权价格与理论发生偏离,使原本合约及合约间的价格平衡遭到破坏,继而产生风险为零,收益恒为正的套利机会。
从理论上来说,在一个高效的市场中,所有市场信息会第一时间反映在价格上,任何资产价格都不会偏离其应有价值,利用价差进行无风险套利的机会应该是不存在的。但大量研究和实践经验表明,现实中的市场并非完全有效市场,不同资产价格之间有可能在极短时间产生失衡,这就使无风险套利成为可能。
尤其是在成熟度还不高的新兴市场,套利机会仍然大量存在。期权无风险套利主要包括期权的上下边界套利、期权的垂直价差套利、利用凸性关系套利以及买卖权平价套利。
(1)单个期权套利策略
如单个期权价格超出上下限的范围时,就能够通过卖出(买入)期权的同时买入(卖出)标的资产的方法进行无风险套利。
(2)单个期权上限套利
在任何时刻,看涨期权价格都不能超过标的资产价格,即期权价格的上限为标的资产价格。如果看涨期权价格超过标的资产价格,可以卖出看涨期权,同时以现价买进标的资产,从而获取无风险利润。
(3)看涨期权的上限套利
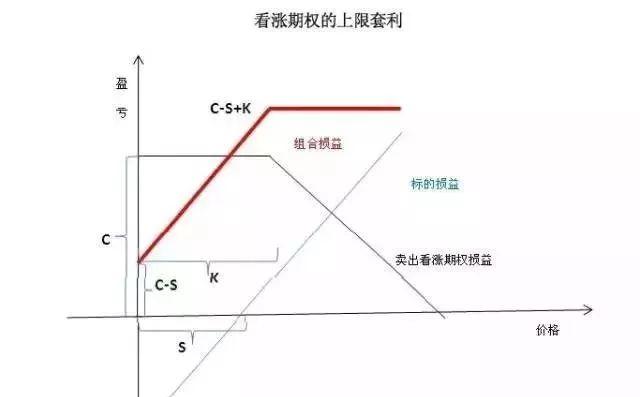
对于欧式看跌期权,任何时刻其价格应该低于其执行价格的贴现值。如果看跌期权价格高于其执行价格的贴现值,可以卖出看跌期权套利(也可将所有收入以无风险利率投资,获取无风险收益)。
单个期权上限套利的损益曲线,类似于将卖出看跌期权的损益曲线全部平移至0轴上方。
(4)看跌期权上限套利
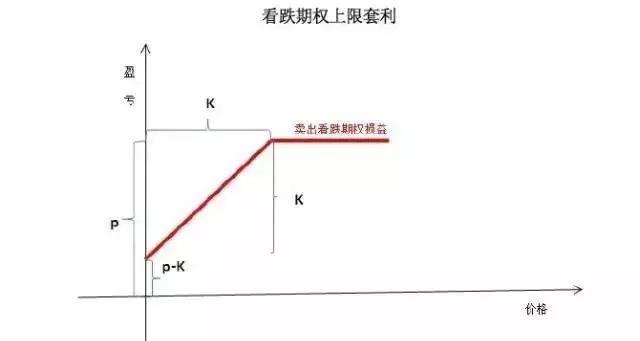
(5)单个期权下限套利
在任何时刻,不付红利的欧式看涨期权的价格应高于标的资产现价与执行价格的贴现值差额与零的较大者。
如果标的资产现价与执行价格的贴现值差额大于0,且看涨期权的价格低于资产现价与执行价格的贴现值差额,则可以进行看涨期权下限套利,即买入看涨期权,同时卖出标的资产而获得无风险利润。看涨期权下限套利的损益曲线,类似于将买入看跌期权的损益曲线全部平移至0轴上方。
(6)看涨期权下限套利
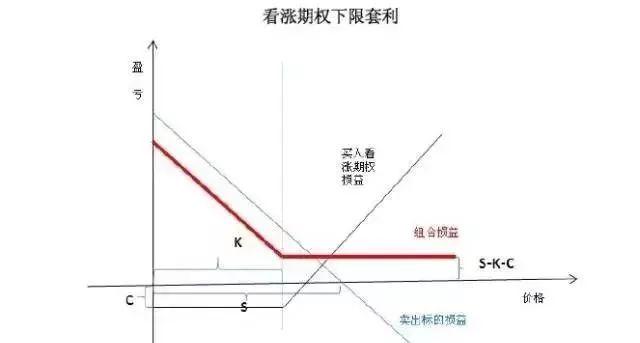
相似地,不付红利的欧式看跌期权的价格应高于执行价格的贴现值与标的资产现价差额与零的较大者。
如果执行价格的贴现值与标的资产现价的差额大于0,且看跌期权价格低于执行价格与标的资产现价的差额,可以进行看跌期权下限套利,即买入看跌期权,同时买入标的资产而获得无风险利润。
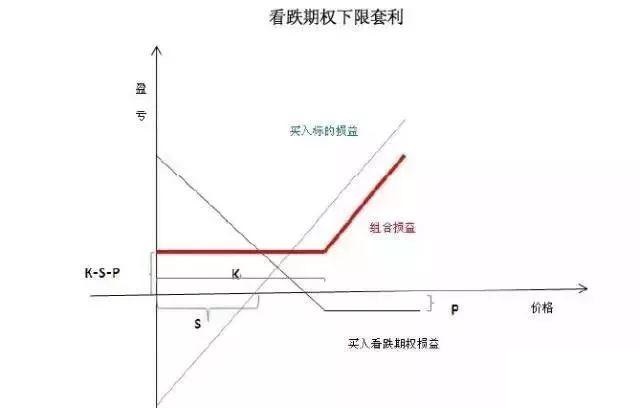
简言之,就是“买低卖高”。看跌期权下限套利的损益曲线,类似于将买入看涨期权的损益曲线全部平移至0轴上方。
(7)看跌期权下限套利
(8)垂直套利策略
对于看涨期权而言,执行价格越高,其他参数相同,期权价格越低;而看跌期权则正好相反。
因此,对于垂直套利策略来说,如果两个执行价格不同的看涨期权合约(或者看跌期权合约)价格不满足上述条件,则该垂直套利策略无风险。
以欧式看涨期权牛市垂直套利为例,较低执行价格看涨期权价格也较低,则卖高执行价期权同时买低执行价期权构成无风险套利策略。
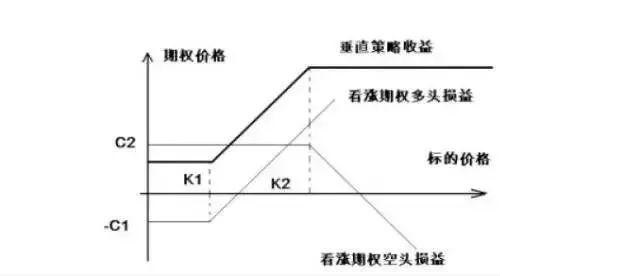
由于C2>C1 ,该垂直策略初始现金流为正值,即C2-C1>0 ,并且无论到期标的资产价格为何值,该垂直策略都保证不小于C2-C1的收益。
垂直套利的其他几种策略都可以类似找出无风险套利机会。
(9)蝶式套利策略
买入蝶式套利(Long Butterfly)
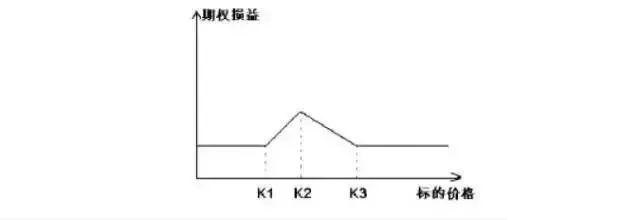
该策略买入一份低执行价格和一份高执行价格期权合约的同时,卖出两份中间执行价格的期权合约。其损益图为:
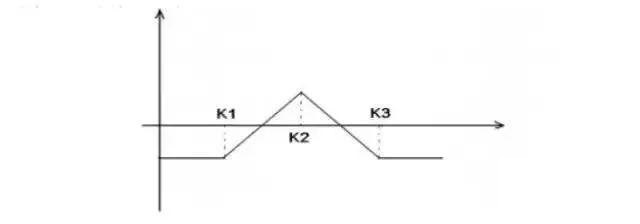
从损益图可以看出,该策略在标的价格偏离比较大时,出现亏损。
如果期权在交易过程当中,执行价格相邻的三份合约出现了价格背离平衡,就是执行价格为K2的合约被高估(相对于K1、K3而言)。那么所谓的价格平衡是一种怎样的形式?因为Gamma 值为期权价格关于标的资产价格的二次偏导数,且Gamma恒为正值,即曲线是凸的。
接下来利用期权价格曲线的凸性,搜寻将蝶式套利策略转化为无风险套利的条件。为此,绘制期权价格关于执行价格的关系曲线示意图。
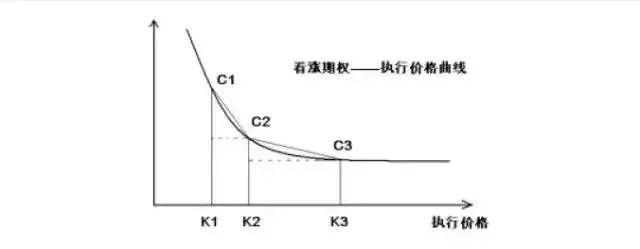
根据价格曲线的凸性,图中C1C2段斜率绝对值要大于C2C3段斜率的绝对值。
转化成数学的关系式即为:
(C1-C2)/(K2-K1)>(C2-C3)/(K3-K2)
即:
(K3-K2)/(K3-K1)*C1+ (K2-K1)/(K3-K1)*C3>C2
观察不等式,可以发现不等式两边分别为 C1、C3 和C2 ,已经十分接近蝶式套利的架构。(如果执行价格间距相等,则形式和蝶式套利一致。)当期权的价格满足时,就可获得无风险套利机会。
具体策略:
买入(K3-K2)/(K3-K1)单位的C1和(K2-K1)/(K3-K1)单位的C3,同时卖出1个单位的C2。
由于(K3-K2)/(K3-K1) + ( K2-K1)/( K3-K1)=1,则期权到期损益图中,当标的资产价格超过K3时,
期权损益为一固定值,且该值与标的资产小于K1 时的期权损益值一致。根据假设,可知该固定值正好为卖出期权与买入期权的价差:
C2-(K3-K2)/(K3-K1)*C1+ (K2-K1)/(K3-K1)*C3
由于该种情形执行价格的间距不一定相等,因此损益图不像蝶式套利那样关于中间执行价格对称。
对于看跌期权的蝶式买入套利策略,依照同样的分析方法,可以找到无风险套利的机会以及无风险套利的策略。
卖出蝶式套利(Short Butterfly)
该策略卖出一份低执行价格和高执行价格期权合约的同时,买入两份中间执行价格的期权合约,其损益图为:
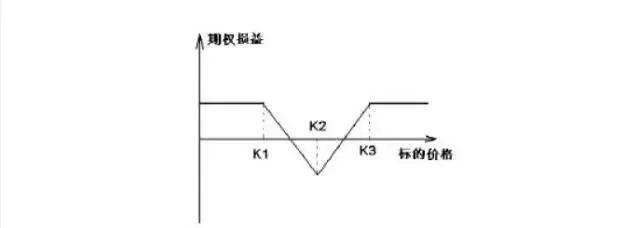
从损益图可以看出,标的资产价格偏离中间执行价格较小时,策略的损失达到最大。而标的价格远离中间执行价格时,该策略为投资者带来固定收益。
以看涨期权为例,根据上一段的分析,若不等式
(K3-K2)/(K3-K1)*C1+ (K2-K1)/(K3-K1)*C3>C2
成立,则前述的买入蝶式套利方式的无风险套利机会不存在。但是,若卖出套利策略的损益图向上平移若干个单位,则可以使得期权到期损益曲线完全位于横轴上方,该种情况下卖出蝶式策略称为无风险套利。
而损益曲线的向上平移,意味着策略的初始现金流入增加,即将 C1、C3 与C2 的价差扩大。至于价差满足怎样的关系式,由下面示意图给出:
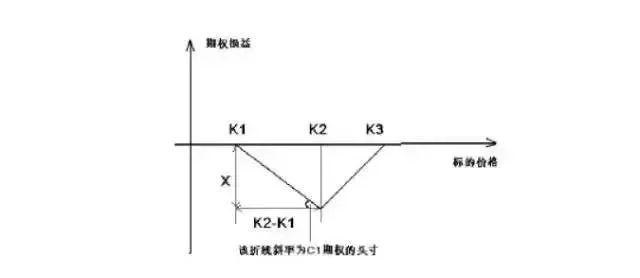
通过上图,可以得出:X=(K2- K1)* C1的头寸。
考虑如下差价关系:
(K3-K2)/(K3-K1)*C1+ (K2-K1)/(K3-K1)*C3-C2>(K3-K2)/(K3-K1)*(K2-K1)
如果将C1的头寸设为(K3-K2)/(K3-K1)单位的空头,则通过不等式左边构建出来的策略,其损益图完全位于横轴上方。
无风险套利策略:卖出(K3-K2)/(K3-K1)单位C1、(K2-K1)/(K3-K1)单位C3,同时买入一份C2。对于看跌期权的蝶式卖出套利策略,依照同样的分析方法,可以找到无风险套利的机会以及无风险套利的策略。
(10)飞鹰式套利策略
买入飞鹰式套利(Long Condor)
该策略涉及 4 个期权合约,在买入一个低执行价格和一个高执行价格期权合约的同时,卖出两个中间执行价格(两个执行价格不同)的期权合约,并且执行价格间距相等。该策略的损益图为(看涨期权):
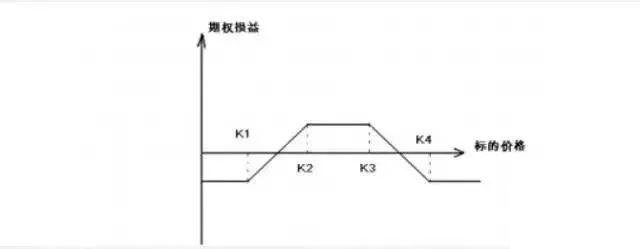
从损益图看,飞鹰式套利与蝶式套利十分类似,区别就在于中间执行价格期权合约的选择。接下来用类似于寻找蝶式无风险套利的方法,搜寻 4 个期权合约之间存在的无风险套利机会。
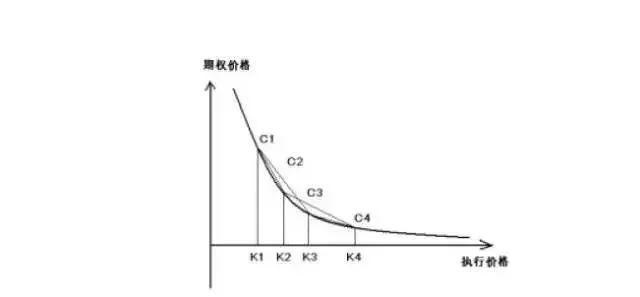
根据期权价格的凸性,可知:
(K4-K2)/(K4-K1)*C1+ (K2-K1)/(K4-K1)*C4>C2
(K4-K3)/(K4-K1)*C1+ (K3-K1)/(K4-K1)*C4>C3
将其相加,得到:
(2K4-K3-K2)/(K4-K1)*C1+ (K2+K3-2K1)/(K4-K1)*C4>C2+C3
如果
(2K4-K3-K2)/(K4-K1)*C1+ (K2+K3-2K1)/(K4-K1)*C4 < P
就可获得无风险套利机会。
具体策略:
买入(2K4-K3-K2)/(K4-K1)单位的C1和(K2+K3-2K1)/(K4-K1)单位的C4,同时卖出1个单位的C2、C3。
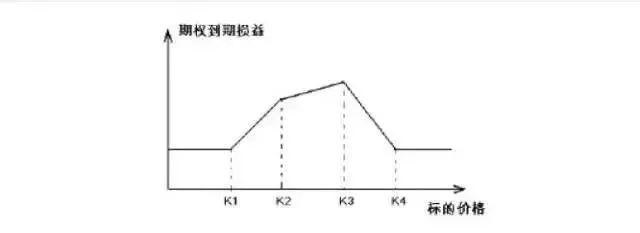
从上图可知,无论到期时,标的资产价格落在哪个区间范围,策略都保证非负收益,因此为无风险策略。对于看跌期权的买入飞鹰式套利,用同样的方法可以进行分析。
卖出飞鹰式套利(ShortCondor)
该策略在卖出一份高执行价格和低执行价格期权合约的同时,买入两份中间执行价格(两个执行价格不同)的期权合约,并且执行价格距离相等。其损益图(看涨期权)为:
可以看出,只要期权初始现金流入量高于MAX(X1,X2) ,就可以保证策略无风险。其中:
X1=(K2- K1)* C1的头寸,X2=(K2- K1)* C4的头寸。
而,飞鹰式套利策略4个期权合约价格满足:
(2K4-K3-K2)/(K4-K1)*C1+ (K2+K3-2K1)/(K4-K1)*C4>C2+C3
即:
(2K4-K3-K2)/(K4-K1)*C1+ (K2+K3-2K1)/(K4-K1)*C4-(C2+C3)>0
假如不等式左边的值太大,则会产生如蝶式套利。即当
(2K4-K3-K2)/(K4-K1)*C1+ (K2+K3-2K1)/(K4-K1)*C4-(C2+C3)>max(X1,X2)
X1 = (K2-K1)*(2K4-K3-K2)/(K4-K1)
X2 = (K4-K3)*(K2+K3-2K1)/(K4-K1)
时,就会出现无风险套利机会。
策略:
卖出(2K4-K3-K2)/(K4-K1) 份C1和 (K2+K3-2K1)/(K4-K1) 份C4,买入1份C2和1份C3。
从上图可知,无论到期时,标的资产价格落在哪个区间范围,策略都保证非负收益,因此为无风险策略。对于看跌期权的卖出飞鹰式套利,用同样的方法可以进行分析。
除了前述的通过期权的经典套利策略搜寻无风险套利机会之外,还有其他的无风险套利机会。
(11)买卖权平价套利
期权平价关系是指,任何时刻相同执行价格的看涨期权与看跌期权之间存在一种均衡关系,即对于同一标的、同一到期日、相同执行价格的看涨和看跌期权,在特定时间里看涨期权与看跌期权的差价,应该等于标的资产现价与期权执行价格贴现值之差,即:
C-P=S-Ke-rT,该性质称为Put-Call Parity。
如果该等式一旦变成不等式,则可以通过卖出不等式两边价格较高的资产组合同时买入价格较低的资产组合的方式来进行无风险套利。
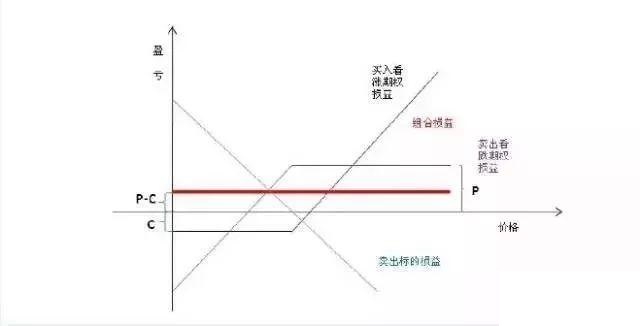
可以将看涨期权与看跌期权的差价视为组合A,将标的资产现价与期权执行价格贴现值之差视为组合B。当A≠B时,可以通过买低卖高获得两者的价差收益。买卖权平价套利的损益曲线是一条水平的直线,且位于0轴上方。
基于Put-Call Parity的无风险套利策略可以理解为:通过期权复制现货的方式在期权、现货两个市场之间进行无风险套利。
如果同时买入一手看跌期权和卖出一手同行权价的看涨期权,假设C是看涨期权权利金,P是看跌期权权利金,K是共同的行权价,因为该组合共支付了P-C的成本,因此损益平衡点K-(P-C)才是“复制”所得标的物空头的真正“卖出价”。
如果上述期权组合“复制”出的标的物空头价格比实际价格贵,也可以在期权和标的物两个市场上赚差价,在买入看跌期权和卖出同数量同行权价看涨期权的同时做多同数量的标的物。
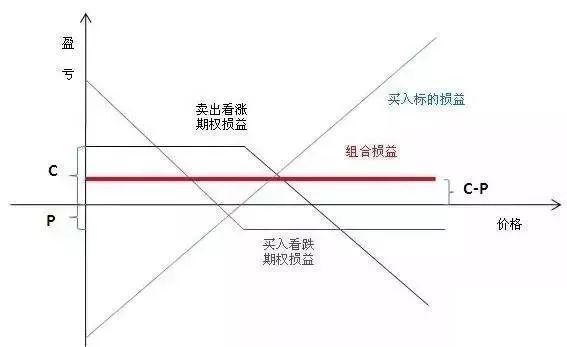
除了复制标的物空头,期权还能复制多头。若买入看涨期权C,则行情上涨时盈利,同时再卖出同行权价的看跌期权P,行情下跌就会亏损,于是就完美复制出了标的物多头。
由于共支付了C-P的净权利金,因此复制品的买入价为K+C-P。若标的物市场上的实际价格高于复制品,就可以从期权市场“买”标的物,同时在标的物市场上卖出,从而赚取无风险的差价,即买入看涨期权并卖出同行权价同数量看跌期权的同时,做空同行权价的标的物。
(12)箱式套利
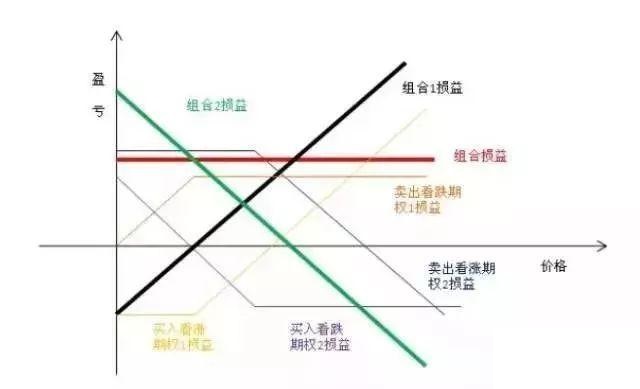
箱式套利又称盒式套利,是由一个牛市价差组合和一个熊市价差组合构成。箱型差价关系是建立在牛市差价期权与熊市差价期权之间的无套利原则之上。
根据换言之,较低执行价格看涨期权价格与较高执行价格看涨期权价格之差,加上较高执行价格看跌期权价格与较低执行价格看跌期权价格之差,应当等于较高执行价格与较低执行价格之差的贴现值。即:
C1-C2+P2-P1= K2e-rT–K1e-rT,也就是C1-P1+K1e-rT =C2-P2+ K2e-rT。
当C1-P1+K1e-rT≠C2-P2+K2e-rT时,可以通过买低卖高获得两者的价差收益。
03
期权套利机会和组合构建原则
期权无风险套利是一种理想化的期权交易方式,旨在实现严格意义上的套利,即通过适当的期权组合在期权市场上实现无风险的利润。
从某种程度上来讲,无风险套利的目标是在期权市场上享受“免费的午餐”,但套利的机会较少,往往在一些特殊的情况下才有可能发生。
随着参与套利的投资者不断增多,以及机构自动化交易系统的成熟,新兴市场的套利机会及空间也将不断减小。从国际成熟市场的经验来看,后期把握套利机会主要依靠较低的交易费用和较高的下单速度,目前成熟市场中仅做市商或专业的交易员才有资源去获得期权套利机会。
套利能赚取无风险的收益,各类投资者必全力争夺,即便套利机会如流星般闪现,也会被各种“全自动刷票软件”抢走。
在行情波动剧烈的时间段,这类机会尤其容易出现,但也稍纵即逝。因此,在真实行情中这种机会一般很难被散户投资者获取。
一般来说,在构造期权无风险套利时,应当遵循两条基本原则:
一是买低卖高原则,即买进价值被低估的期权,卖出价值被高估的期权;
二是风险对冲原则,即利用合成期权对冲买入或卖出实际期权的风险头寸。
若要在期权市场上进行套利活动,套利者首先要根据期权价格规律即时捕捉到任何可能的套利机会,即被错误定价的期权,然后根据上面两个原则来构造无风险套利组合。
04
期权激励
激励功能是由期权的盈利功能延伸出来的一项功能。
在现代公司制的条件下,公司主管人员怎样激励经营管理人员为所有者工作,即如何调动他们的积极性,这是关系到公司发展的一个重大问题。
一些公司的所有者往往用期权作为激励经营管理人员的工具,已取得了较好的效果。他们给予经营管理人员较长期限内的该公司股票的买入期权,合约规定的买入价一般与当时的股价接近。
这样公司经营管理人员只要努力工作使企业经济效益不断提高,服票价格也会随之上扬,股票买入期权的价格同样会上升,经营管理人员便可从中获利。因为,规定的期限较长,这种激励方式通常有较好的持久性,对防止经营管理人员的短期行为十分有利。
05
期权的风险对冲
对于投资机构而言,发行期权(即成为期权的卖方)需要做很多的基础研究——既然要承担风险(期权卖方处在一个长期承担无限风险的处境),就必须知道风险敞口是多少。
在建立了期权卖方仓位后,除了硬挺着(这也是一种常见策略),期权卖方还可以通过交易策略对冲掉部分的风险。
对冲策略被广泛运用于期权市场的参与者(例如做市商),计算并分析期权组合的希腊值(又称风险指标)之后,采取相应的对冲策略。
鉴于期权价值对标的资产的价格及其波动率最为敏感,而delta中性策略仅能规避价格因素对投资组合的影响,本文侧重介绍如何在对冲过程中同时规避标的现货价格及其波动率等因素,相关的希腊值主要包括delta、gamma和vega。
(1)Delta对冲
Delta对冲又称delta中性策略,对冲后的期权头寸价值受标的资产价格小幅变动的影响较小,该策略主要用于规避方向性风险。例如,假设某投资者购入10手认购期权A,每手对应的delta值为0.5,同时卖出20手delta值为-0.3的认沽期权B,如表1所示每手期权对应100份标的。

那么,该期权组合的delta值为:500+600=1100
因此,投资者通过卖出1100份标的现货将该组合的头寸调整为delta中性。
(2)Delta-Gamma对冲
由于每份期权的delta值并非固定不变,而是随标的资产价格的变化而改变,投资者需要不断进行对冲。
对冲过程中,若将期权头寸的gamma值考虑在内,可有效减少对冲误差。与delta对冲方式不同,gamma对冲主要通过买入或卖出期权而不是标的资产的形式完成。
假设某投资者购入10手delta和gamma值分别为0.8和0.3的认购期权A,该投资者考虑通过交易相同标的的认购期权B进行delta-gamma对冲,该期权的delta和gamma值分别为0.4和0.2,如表2所示。
每手期权对应100份标的,假设gamma对冲需要交易X手认购期权B。

那么投资者通过卖出15手期权B的方式来实现头寸的gamma对冲:+300+(-15)×20=0
此时,该期权组合的delta值为+200:+800+(-15)×40=+200
那么,投资者需要卖出200份标的现货,使得组合保持delta-gamma中性。
(3)Delta-Gamma-Vega对冲
当期权组合处于delta-gamma中性下,尽管期权组合价值受标的资产价格变化的影响较小,但受标的资产价格波动的影响显著。通过Delta-Gamma-Vega对冲,可同时降低两个因素的影响。
假设某投资者购入10手delta、gamma和vega值分别为0.8、0.3和0.2的认购期权A。投资者考虑通过交易同一标的的认购期权B和认沽期权C来实现Delta-Gamma-Vega对冲。
认购期权B的delta、gamma和vega值分别为0.4、0.2和0.1,认沽期权C的delta、gamma和vega值分别为-0.6、0.3和0.1,如表3所示。每手期权对应100份标的,假设投资者需要交易X份认购期权B和Y份认沽期权C。
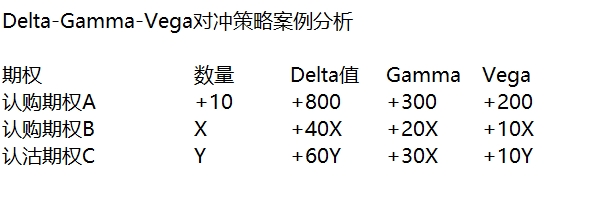
当300+20X+30Y=0时,组合的gamma值为0。
当200+10X+10Y=0时,组合的vega值为0。
因此,通过卖出30手认购期权B和买入10手认沽期权C,期权头寸实现gamma-vega中性,而此时的delta值为:
+800+(-30)×40+10×(-60)=-1000
那么,投资者需要买入1000份标的现货以实现Delta-Gamma-Vega中性。
在标的资产价格小幅变动时,文中提及的三种策略可以有效规避头寸风险,delta-gamma策略在标的资产价格变化较大时,不但对冲效果显著,还可以获得价格波动带来的收益。
在对冲过程中,先通过买入或卖出期权将gamma和vega值调整为0,随后通过买入或卖出标的现货调整delta至中性。
在实际应用时,投资者可以选择定期调仓的静态对冲策略或者也可考虑根据风险承受能力,待希腊值超出预定的阀值时再进行动态对冲。
但是需要注意的是,所谓中性,事实说在构造头寸之初投资组合的一个或者几个变量是中性的,随后而来的变化可能会对这种中立性产生不利的影响。
即使我们使得delta,gamma,vega,theta,rho都达到中性状态,也只能是某一时刻上的中性,他们针对的只是价格发生微小变化的情况,当价格发生剧烈变动这些希腊字母并不适用。
除了delta、gamma和vega值外,投资者同样需要注意和分析其他希腊值(如theta、rho和volga等),以及选择流动性较好的期权进行对冲,做好相关的风险管理措施。
浏览数:3327